向量

向量是一个抽象的数学概念,只要满足一个向量经过数值放缩之后仍是一个唯一向量和两个向量经过向量加法可以得到一个唯一向量那么就可以视作向量,如此,所有的线性变换对这个定义下的向量都适用,这在建模的时候会很有用,比如将函数视为向量
也就是说只要定义好向量的形式,向量的数乘方法和向量加法就可以对其使用线性代数的工具,需要注意的是,定义的方法需要使下面等式成立 v⃗ + v⃗ = 2v⃗
向量空间
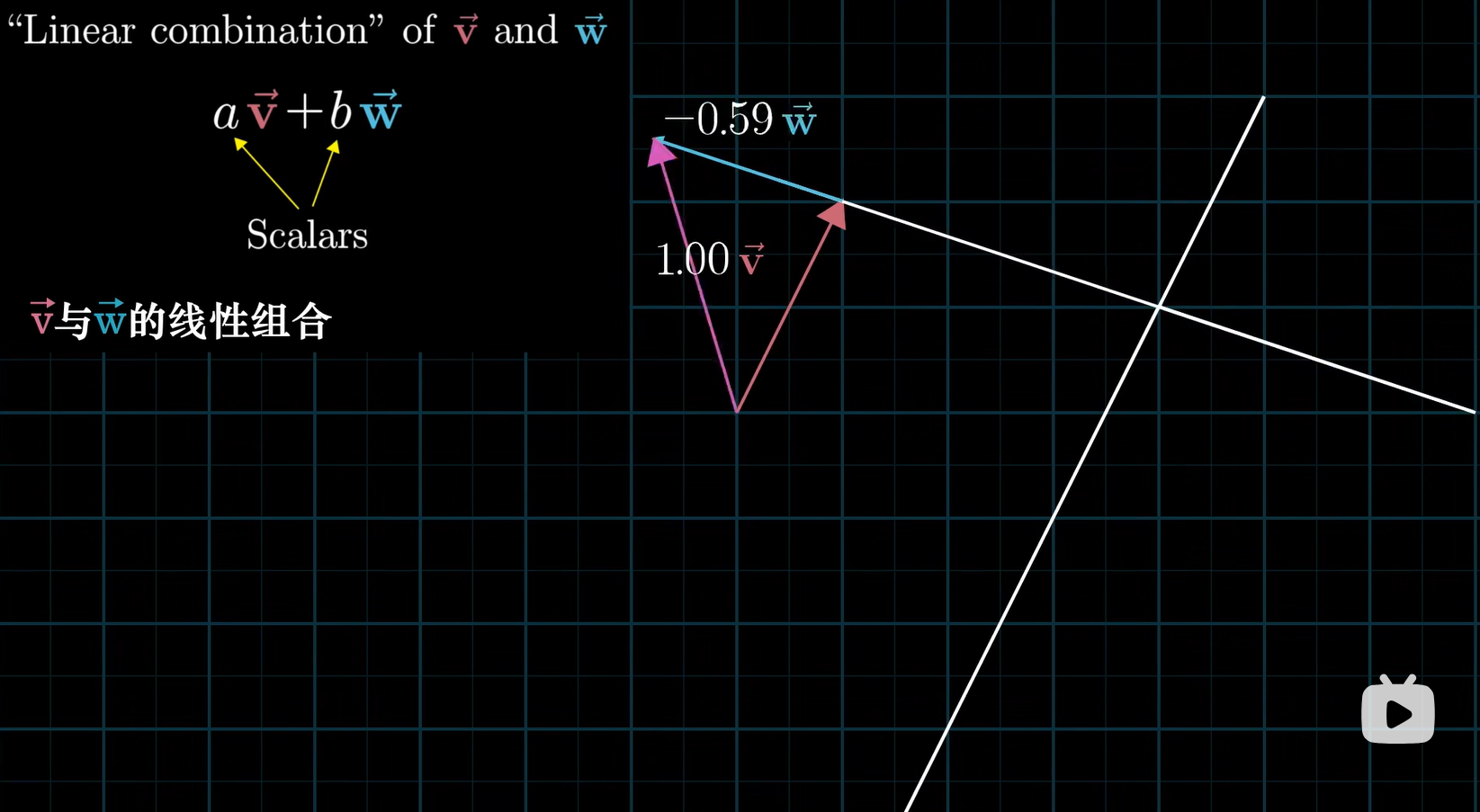
向量空间是通过选择的基底向量进行线性组合张成的空间,有几个线性无关的基底向量这个空间就有多少个维度,需要注意的是当使用坐标表示向量时,有几个坐标维度这个空间就有几个维度
矩阵
矩阵有几个视角
矩阵是一个向量空间
把矩阵看作是向量列表,那么矩阵就是以这些向量为基底向量张成的向量空间,矩阵的秩就是向量空间的维度 $$ \mathbf{W}=[\vec{v_{1}},\;\vec{v_{2}}...] $$
矩阵是一个线性变换
把矩阵看作是一个关于向量的变换,其内容是同在某个空间的向量的采样集合,其输入是维度大小与矩阵中向量数量相等的空间中的向量,输出是输入向量在矩阵所在的向量空间中的投影,变换内容可以理解为将输入空间的单位正交基底变换成矩阵中对应的向量的空间变换
如: $$ \begin{bmatrix} 1 & 1 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 7 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} $$ 在这个式子中我们将最左边的矩阵视为一个变换,这个矩阵由3维空间中采样的2个向量组成,输入是2维空间中的2个向量,输出是这2个向量在矩阵所在的3维空间的投影,实际上这个变换的意思就是将一个2维空间压缩映射到3维空间中的一个轴上
矩阵乘法与复合矩阵
以矩阵是一个变换的角度去看矩阵乘法 ABv⃗ = Cv⃗ 如果上式成立,那么意味着对向量进行C变换,应该与先进行B变换再进行A变换的结果一致,则称矩阵C是矩阵A、B的复合矩阵,类似于复合函数 f(g(x)) = f ⋅ g(x) 所以矩阵乘法可以看作是复合矩阵变换的做法,要注意乘法的顺序
行列式
矩阵(仅限方阵)的行列式det(A)表示的是矩阵所代表的变换,对原空间的缩放比例,符号代表空间的取向与原空间是否相同,利用行列式的绝对值能够快速计算变换后的测度(如面积、体积等)
