跳表

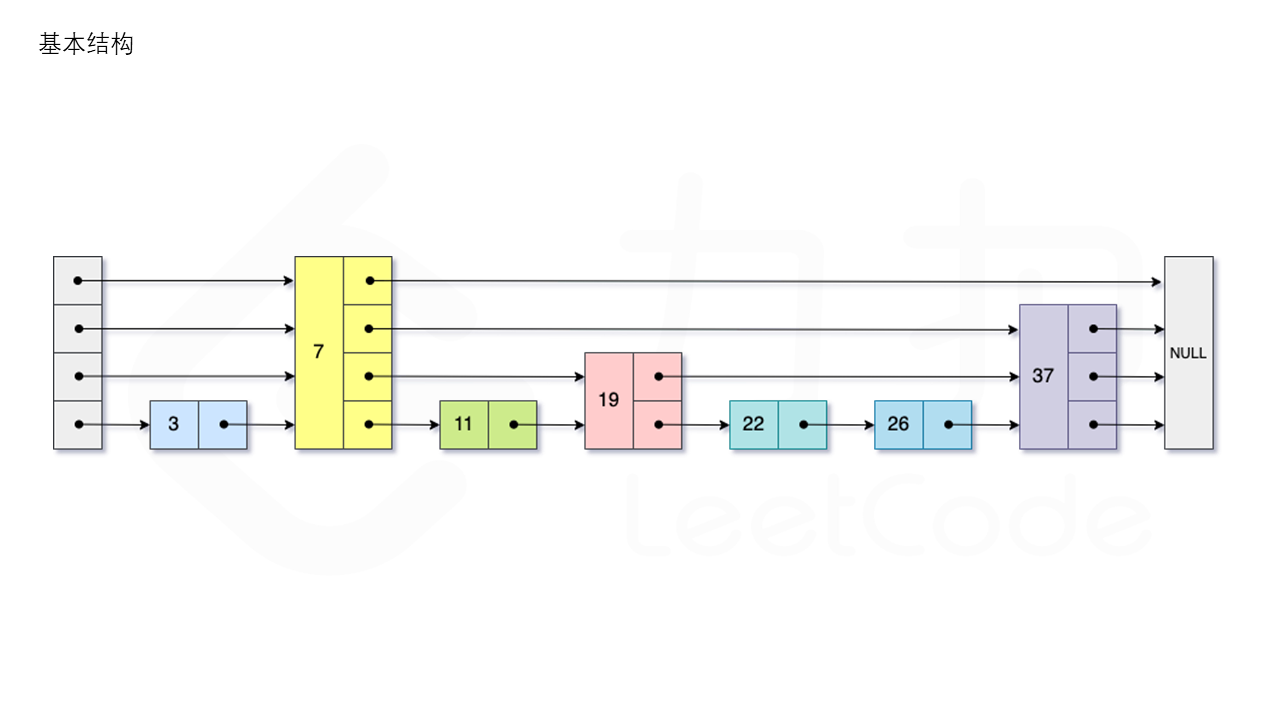
结构

跳表的期望空间复杂度为O(n)，跳表的查询，插入和删除操作的期望时间复杂度均为O(logn)。跳表实际为一种多层的有序链表，跳表的每一层都为一个有序链表，且满足每个位于第i层的节点有p的概率出现在第i+1层，其中p为常数。

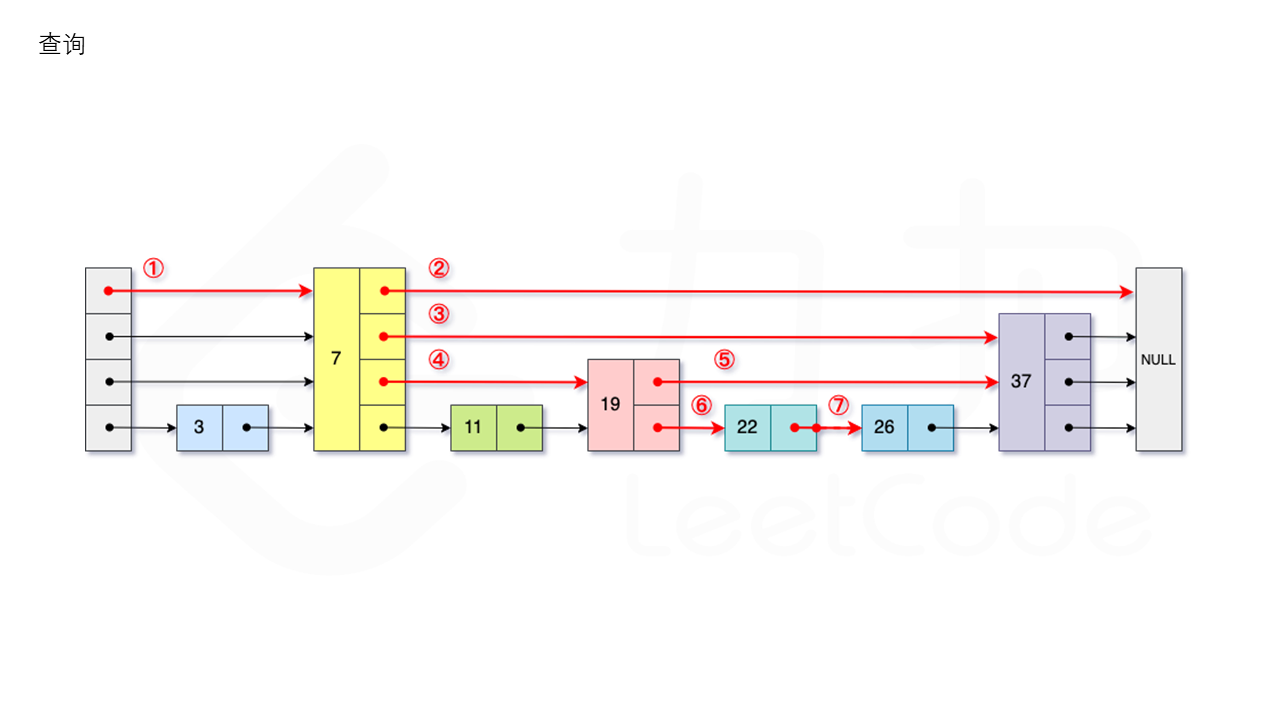
查询

从跳表的当前的最大层数level层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第1层。此时，若第1层的下一个节点的值等于target，则返回true；反之，则返回false。如图所示：

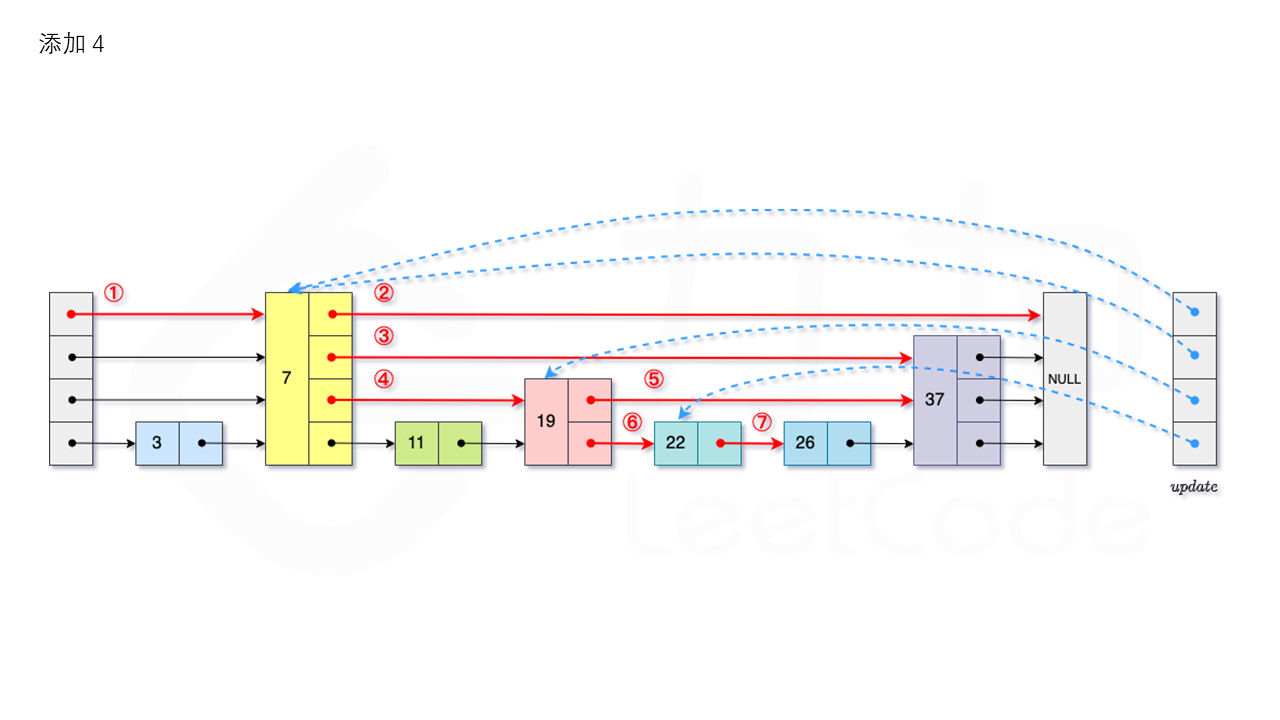
添加

从跳表的当前的最大层数level层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第1层。设新加入的节点为newNode，我们需要计算出此次节点插入的层数lv，如果level小于lv，则同时需要更新level。我们用数组update保存每一层查找的最后一个节点，第i层最后的节点为update[i]。我们将newNode的后续节点指向update[i]的下一个节点，同时更新update[i]的后续节点为newNode。如图所示：

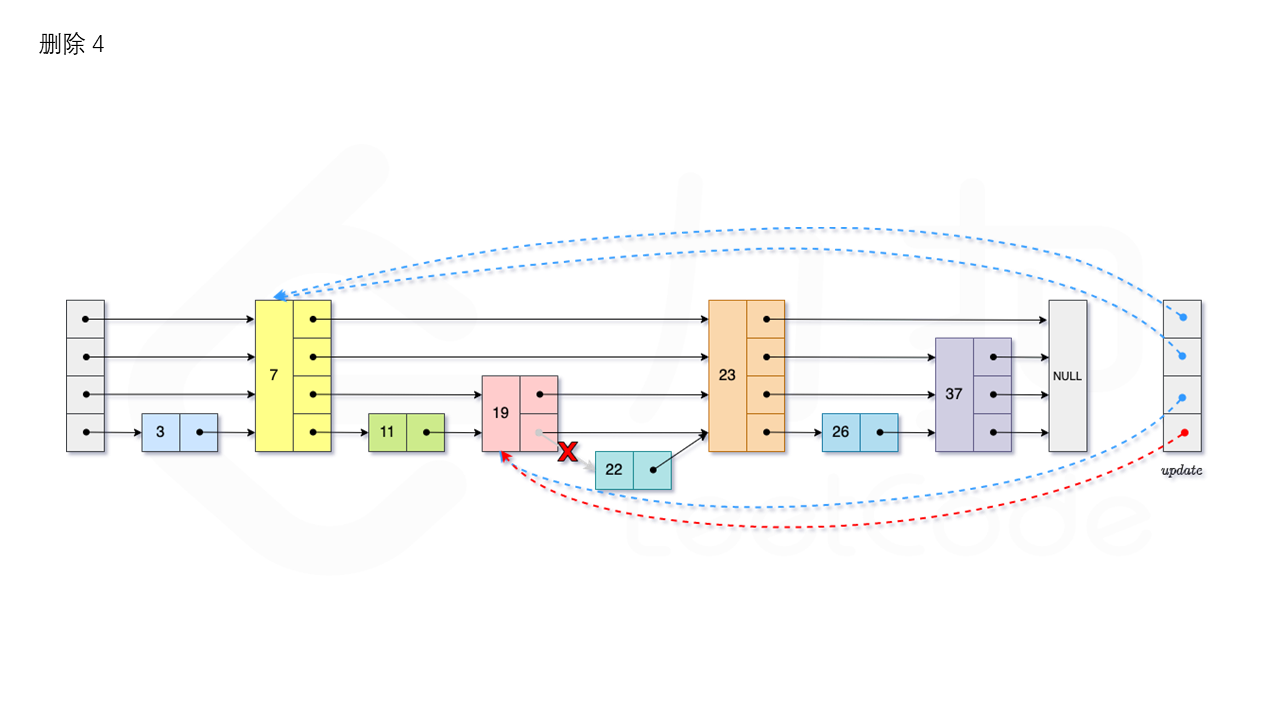
删除

首先我们需要查找当前元素是否存在跳表中。从跳表的当前的最大层数level层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第1层。如果第1层的下一个节点不等于num时，则表示当前元素不存在直接返回。我们用数组update保存每一层查找的最后一个节点，第i层最后的节点为update[i]。此时第i层的下一个节点的值为num，则我们需要将其从跳表中将其删除。由于第i层的以p的概率出现在第i+1层，因此我们应当从第1层开始往上进行更新，将num从update[i]的下一跳中删除，同时更新update[i]的后续节点，直到当前层的链表中没有出现num的节点为止。最后我们还需要更新跳表中当前的最大层数level。如图所示：

空间复杂度分析

每次添加节点时，节点出现在第i层的概率为\((1-p)×{p}^{i-1}\)，跳表插入时的期望层数为:
\[ E(L)=\sum_{i=1}^{\infin}i×(1-p)×{p}^{i-1}=\frac{1}{1-p} \]

如果节点的目标层数为L，则此时需要的空间为O(L)，因此总的空间复杂度为\(O(n×E(L))=O(n×\frac{1}{1-p})=O(n)\)。

时间复杂度分析

在含有n个节点的跳表中，当前最大层数L(n)包含的元素个数期望为\(\frac{1}{p}\)，根据跳表的定义可以知道第1层的每个元素出现在L(n)的概率为\({p}^{L(n)-1}\)，则此时我们可以推出如下：
\[ \frac{1}{p}=n{p}^{L(n)-1} \]
根据以上结论可以知道在含有n个节点的跳表中，当前最大层数期望\(L(n)={log}_{p}\frac{1}{n}\)

令C(i)为在一个无限长度的跳表中向上爬i层的期望代价，最小代价即为往左上角爬，根据定义，则知道:
\[ \begin{gather} C(0)=0 \\ C(i)=(1-p)(1+C(i))+p(1+C(i-1)) \\ C(i)=\frac{i}{p} \end{gather} \]
在含有n个元素的跳表中，从第1层爬到第L(n)层的期望步数存在上界\(\frac{L(n)-1}{p}\)，当达到第L(n)层后，我们需要向左走。我们已知L(n)层的节点总数的期望存在上界为\(\frac{1}{p}\)，所以平均查询时间复杂度为\(\frac{L(n)-1}{p}+\frac{1}{p}=\frac{log_{\frac{1}{p}}n}{p}=O(log\ n)\)

实现细节

每个跳表节点保存一个值以及下一列的地址

class Skiplist {
    
    // 最大层数
    static final int MAX_LEVEL = 32;
    // 下一层留存概率
    static final double P = 0.5;
    // 哨兵节点
    private SkiplistNode head;
    // 当前最大层数
    private int level;
    // 用于插入时随机分配层数
    private Random random;

    public Skiplist() {
        this.head = new SkiplistNode(-1, MAX_LEVEL);
        this.level = 0;
        this.random = new Random();
    }
    
    public boolean search(int target) {
        SkiplistNode cur = this.head;
        // 从最高层开始向下查找
        for (int i = this.level - 1; i >= 0; i--) {
            // 在当前层从左往右查找不大于target的最大节点
            while (cur.forward[i] != null && cur.forward[i].val < target) {
                cur = cur.forward[i];
            }
        }
        // 下一节点
        cur = cur.forward[0];
        if (cur != null && cur.val == target) {
            return true;
        }
        return false;
    }
    
    public void add(int num) {
        // 保存每层需要更新下一节点的列地址
        SkiplistNode[] update = new SkiplistNode[MAX_LEVEL];
        Arrays.fill(update, this.head);
        SkiplistNode cur = this.head;
        for (int i = this.level - 1; i >= 0; i--) {
            while (cur.forward[i] != null && cur.forward[i].val < num) {
                cur = cur.forward[i];
            }
            update[i] = cur;
        }
        int lv = this.randomLevel();
        // 更新层数
        this.level = Math.max(this.level, lv);
        SkiplistNode newNode = new SkiplistNode(num, lv);
        // 更新列
        for (int i = 0; i < lv; i++) {
            newNode.forward[i] = update[i].forward[i];
            update[i].forward[i] = newNode;
        }
    }
    
    public boolean erase(int num) {
        SkiplistNode[] update = new SkiplistNode[MAX_LEVEL];
        SkiplistNode cur = this.head;
        for (int i = this.level - 1; i >= 0; i--) {
            while (cur.forward[i] != null && cur.forward[i].val < num) {
                cur = cur.forward[i];
            }
            update[i] = cur;
        }
        cur = cur.forward[0];
        // 不在跳表里
        if (cur == null || cur.val != num) {
            return false;
        }
        for (int i = 0; i < this.level; i++) {
            if (update[i].forward[i] != cur) {
                break;
            }
            update[i].forward[i] = cur.forward[i];
        }
        // 更新层数
        while (this.level > 1 && this.head.forward[this.level - 1] == null) {
            this.level--;
        }
        return true;
    }

    private int randomLevel() {
        int lv = 1;
        while (random.nextDouble() < P && lv < MAX_LEVEL) {
            lv++;
        }
        return lv;
    }
    
}

class SkiplistNode {
    
    // 节点值
    int val;
    // 下一列的地址
    SkiplistNode[] forward;

    public SkiplistNode(int val, int maxLevel) {
        this.val = val;
        this.forward = new SkiplistNode[maxLevel];
    }
    
}